Nash trovis metodon, kiu donas por ĉiu dupersona ludo kun miksitaj strategioj solvon, kiu plenumas liajn kvin aksiomojn. Sed aksiomojn eblas anstataŭigi per aliaj, kaj efektive kelkaj esplorantoj faris tion.
Kalai en 1977 proponis rezigni pri la aksiomo de lineareco. Anstataŭe li postulis, ke ĉiu ludanto egale profitu de la solvo, kompare al la strikte konkura strategio, kiun ni por niaj konsideroj metis en la originon (0,0). Oni nomas tiun solvon ankaŭ la "egaleca" solvo. En tiu sistemo la solvo de Kalai do estas sur la duoniganto de la unua kvadranto. Por simetriaj ludoj ĝi egalas al la solvo de Nash, sed por nia ekzemplo de nesimetria batalo de la seksoj ĝi donus la solvon (7/4;7/4), kompare al la solvo (7/2;7/6) de Nash.
Por laŭeble profiti el la solvo de Nash, ludantoj povis manipuli la rilaton inter siaj pagoj. Por profiti el la solvo de Kalai ili povas multipliki siajn pagojn tiel, ke ilia preferata pura strategio trafu la duoniganton. Evidente la alia ludanto povas kontraŭbatali tion per multiplikado de siaj propraj pagoj, do denove ni estas en ne-stabila meta-ludo.
La egaleca solvo eliras de la minimumaj pagoj. Plia solvo, kies aksiomojn Kalaj kaj Smorodinski formulis en 1975, konsideras la maksimume (individue, ne samtempe) eblajn pagojn kaj postulas, ke la solvo maksimumigu la pagojn konservante la rilatojn de la maksimume eblaj pagoj. Punkto, kiu kunigas la maksimume eblajn pagojn, nomiĝas ideala punkto; tiu punkto normale ne estas atingebla, alie la interkonsento estus facila. La propono de Kalai kaj Smorodinski egalas la postulon, ke la solvo estu sur rekto tra la origino kaj la ideala punkto.
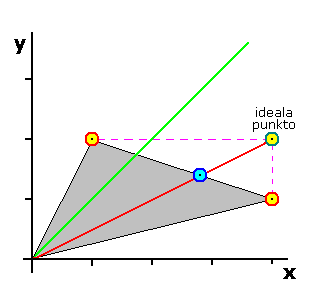
Se la ludantoj povas mem difini siajn subjektivajn pagojn, ili profitas de pagoj, kiuj estas altaj por la de ili preferataj punktoj kaj malaltaj por aliaj. La bildo montras, ke profitis la ludanto, kiu difinis siajn pagojn en la rilato 4:1, kompare al la alia kun rilato 2:1.
La ekzisto de pluraj, pli-malpli egale pravigeblaj aksiomaroj certe ne faciligas la trovon de interkonsento en dupersona ludo. Se ekzistas objekta, nedisputebla pagofunkcio, interkonsentita aksiomaro donas solvon. Se eblas disputi pri la komparo inter la pagoj, la solvo estas duba.
Se la pagoj estas ne nur klare difinitaj, sed eŭ en iu formo (ekz. mono) transdoneblaj, eblas interkonsenti pri flankaj pagoj de unu ludanto al la alia, kontraŭ la promeso ludi certan strategion. Tiel eblas atingi maksimuman suman pagon. En nia ĵusa ekzemplo tiun maksimuman suman pagon atingas nur la punkto (4;1), do la preferata strategio de la unua ludanto, strategio certe neniel justa. La unua ludanto devus cedi al la dua 1,5 unuojn, por ke ambaŭ havu 2,5. En la interseksa batalo li eble povus regali la post-koncertan manĝon. Sed nepra kondiĉo estas interkonsento pri la ambaŭflankaj subjektivaj pagoj.
Se interesas vin mallongaj diskutoj pri ludoteoriaj problemoj, legu pri
|
|
komenco
|